 :G1
:G1 G2
G2 (a · b) =
(a · b) =  (a) ·
(a) ·  (b) (a,b
(b) (a,b  G1).
G1).
 :G1
:G1 G2
G2 (a · b) =
(a · b) =  (a) ·
(a) ·  (b) (a,b
(b) (a,b  G1).
A function
G1).
A function  B
B B
B A
A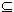 G,
G,
 .
. H,
H, H.
H. G,
G,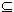 H.
H.| Back | Table of Contents |
|
|
Normal SubgroupsLet us now return to the study of the properties of the subgroups of a group. Our major task will be to introduce the extremely important concept of a normal subgroup. Throughout this section, let G be a group. If A and B are arbitrary subsets of G, let us set
AB = {a · b | a
 A, b A, b  B}. B}.Since multiplication in G is associative, we see that for any subsets A, B, and C of G, we have
A(BC) = (AB)C
We will denote each of these sets by ABC. If
Proposition 1: Let H be a subgroup of G, Proof: From the definition of our notation, we see that
aHa-1 = {aha-1 | h
 H}. H}.
Let  = axa-1 = axa-1 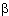 = aya-1. = aya-1.
Now  · ·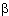 -1=(axa-1)(ay-1a-1) = a(xy-1)a-1 -1=(axa-1)(ay-1a-1) = a(xy-1)a-1  aHa-1. aHa-1.We say that the subgroup aHa-1 is conjugate to H. Usually,
Definition 2: Let H be a subgroup of G. If for every Before giving examples of subgroups which are and are not normal, it is convenient to establish a simple criterion which can be used to determine whether or not a subgroup is normal.
Proposition 3: Let H be a subgroup of G. Then H is normal if and only if for every Proof: Assume first that H is normal. Then for every
bHb-1 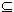 H. H.
However, since
b-1Hb = b-1H(b-1)-1 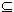 H. H.
Therefore, if
h = bh'b-1  bHb-1. bHb-1.
Since h is any element H, we see that (2)
H 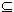 bHb-1. bHb-1.
Therefore, by (1) and (2) we see that
H = bHb-1.
Since our choice for Example 1: If G is any group, {1} and G are both normal subgroups. These normal subgroups are said to be trivial. Example 2: If G is abelian, every subgroup H is normal. For if Example 3: Let
RaHRa
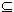 H (a = 0, 1, 2,..., n-1) H (a = 0, 1, 2,..., n-1)
Further since
FRaF-1 = (FRF-1)a = Ra(n-1) (a= 0, 1,..., n-1),
 FHF-1 FHF-1 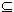 H. H.
Therefore,
(FRa)H(FRa)-1 = F(RaHRa)F-1
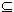 FHF-1 FHF-1 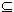 H H
for Example 4: Let
RFR-1 = RFFRF = IRFFRF = F-1FRFFRF
= F-1R-1R-1 = F-1R-2
and since
F-1R-2 = FRn-2.
Since Let H be a subgroup of G and let us consider the sets H\G and G/H of right and left cosets respectively. A typical left coset is a set of the form aH
H · a = aHa-1 · a = aH · 1G = aH.
Thus we have proved
Proposition 4: If H is a normal subgroup, then every right coset Ha of G with respect to H is also a left coset - namely aH; and conversely, every left coset is a right coset. In other words if H is normal, then We will now go through a construction which will appear in various guises a number of times in our study of algebra. So let us try to get some sort of broad insight into the general philosophy which underlies the general philosophy which underlies the construction. The primary mathematical objects we have been discussing so far have been sets. Not just arbitrary sets, however. Our sets in this chapter have been endowed with some extra structure - they are groups. We have already considered the problem of translating this extra structure from the original set to one of its subsets. What we arrived at were subgroups. Now we will consider a similar problem. Suppose that we have an equivalence relation on our original set. Can we translate the structure on the original set to the set of equivalence classes? To be more specific, let us consider a group G and a subgroup H. In or proof of Lagrange's theorem, we considered the equivalence relation on G defined by (*)
a ~ b if and only if ba-1
 H. H.The equivalence classes turned out to be left cosets of G with respect to H. The set of equivalence classes is therefore G/H. In reference to our general question raised above, we can now ask: Can we define a group structure of G/H? Of course we aren't interested in just any group structure on G/H. We are interested in a group structure which is naturally connected with the group structures on G and H. The first law of multiplication which comes to mind is the one defined by (4)
aH · bH = abH.
The very simplicity of this definition leads us to suspect that it should be the "natural" multiplication of G/H. However, we run into problems. It is not in general true that (4) defines a binary operation on G/H. What can go wrong is that the "product" defined by (4) may depend on the choice of a and b and not merely on the cosets aH and bH. However, this difficulty goes away if H is a normal subgroup of G. Let us prove this non-trivial statement. What we claim is that (4) defines a binary operation on G/H in the case where H is a normal subgroup of G. We remarked above that G/H is the set of equivalence classes of G with respect to the equivalence relation ~ defined by (*). Provided that ~ is compatible with multiplication in G, The rules of an equivalence relation imply that (4) defines a binary operation on G/H. This
Theorem 5: Let H be a normal subgroup of G. Then with respect to the rule of multiplication (4), G/H is a group. The identity element is the coset Proof: It suffices to verify the group axioms (G1-G3). Associativity: Identity: Inverse: One further comment about the definition (4) of multiplication of G/H is in order. It is possible to interpret the product Definition 6: Let H be a normal subgroup of the group G. Then the set of cosets G/H with the group structure defined above, is called the quotient group of G modulo H. The term quotient group is used interchangeably with the term factor group. Example 5: Let G denote the group Z with respect to addition, and let Example 6: Let G be the group
H = {f
  | f(0) = 0}. | f(0) = 0}.
Then H is a normal subgroup of G. The elements of G/H are cosets
(f - fa)(0) = f(0) - fa(0)
= a - a
= 0.
Therefore,
G/H = {fa + H | a
 R). R).
It is easy to see that
k:R
 G/H G/H
defined by |
| Back | Table of Contents |